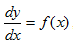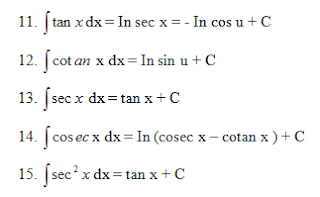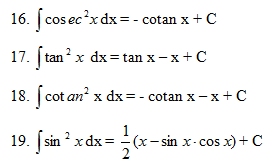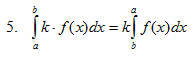Study Ajaib: kalkulus

Tutorial kita kali ini adalah mata pelajaran matematika, dimana kita akan membahas berbagai jenis soal-soal yang berkaitan dengan turunan trigonometri.

Pada tutorial sebelumnya kita telah mempelajari tentang turunan fungsi aljabar, maka dalam kesempatan ini dilanjutkan dengan turunan trigonometri.

Rumus Turunan Dasar Trigonometri

Berikut ini adalah beberapa turunan dasar trigonometri yang wajib diketahui sebelum anda memecahkan persoalan turunan trigonometri:

1. f(x) = sin x → f '(x) = cos x
2. f(x) = cos x → f '(x) = −sin x
3. f(x) = tan x → f '(x) = sec² x
4. f(x) = cot x → f '(x) = −csc²x
5. f(x) = sec x → f '(x) = sec x . tan x
6. f(x) = csc x → f '(x) = −csc x . cot x

Perluasan Rumus Turunan Trigonometri I

Misalkan u merupakan fungsi yang dapat diturunkan terhadap x, dimana u' adalah turunan u terhadap x, maka :

1. f(x) = sin u → f '(x) = cos u . u'
2. f(x) = cos u → f '(x) = −sin u . u'
3. f(x) = tan u → f '(x) = sec²u . u'
4. f(x) = cot u → f '(x) = −csc² u . u'
5. f(x) = sec u → f '(x) = sec u tan u . u'
6. f(x) = csc u → f '(x) = −csc u cot u . u'

Perluasan Rumus Turunan Trigonometri II

Berikut ini adalah turunan dari fungsi-fungsi trigonometri dalam variabel sudut ax +b, dimana a dan b adalah bilangan real dengan a≠0 :

1. f(x) = sin (ax + b) → f '(x) = a cos (ax + b)
2. f(x) = cos (ax + b) → f '(x) = -a sin (ax + b)
3. f(x) = tan (ax + b) → f '(x) = a sec² (ax +b)
4. f(x) = cot (ax + b) → f '(x) = -a csc² (ax+b)
5. f(x) = sec (ax + b) → f '(x) = a tan (ax + b) . sec (ax + b)
6. f(x) = csc (ax + b) → f '(x) = -a cot (ax + b) . csc (ax + b)

Contoh Soal Turunan Trigonometri

Soal No.1

Carilah turunan f'(x) dari fungsi-fungsi trigonometri dibawah ini :
a. f(x) = 4 sin x
b. f(x) = 3 cos x
c. f(x) = -2 cos x
d. f(x) = 2 sec x
e. f(x) = 2 csc x

Pembahasan

a. f(x) = 4 sin x → f'(x) = 4 cos x
b. f(x) = 3 cos x → f'(x) = -3 sin x
c. f(x) = -2 cos x → f'(x) = -2 (-sin x) → f'(x) = 2 sin x
d. f(x) = 2 sec x → f'(x) = 2 sec x . tan x
e. f(x) = 2 csc x → f'(x) = 2 (-csc x . cos x) → f'(x) = -2 csc x . cot x

Soal No.2

Carilah turunan f'(x) dari fungsi-fungsi trigonometri dibawah ini :
a. f(x) = sin 6x + cos 6x
b. f(x) = 3x⁴ + sin 2x + cos 3x
c. f(x) = tan 5x + sec 2x

Pembahasan

a. f(x) = sin 6x + cos 6x → f'(x) = 6 cos 6x - 6 sin 6x
b. f(x) = 3x⁴ + sin 2x + cos 3x → f'(x) = 12x³ + 2 cos 2x - 3 sin 3x
c. f(x) = tan 5x + sec 2x → f'(x) = 5 sec² 5x + sec 2x . tan 2x

Soal No.3

Carilah turunan f'(x) dari fungsi-fungsi trigonometri dibawah ini :
a. f(x) = sin 3x
b. f(x) = sin x²
c. f(x) = sin 3x²
d. f(x) = sin (2x + 1)

Pembahasan

a. f(x) = sin 3x
Misalkan:
u = 3x ⇒ u' = 3
f(x) = sin 3x
f'(x) = cos u . u'
f'(x) = cos 3x . 3
f'(x) = 3 cos 3x

b. f(x) = sin x²
Misalkan:
u = x² ⇒ u' = 2x
f(x) = sin x²
f'(x) = cos u . u'
f'(x) = cos x² . 2x
f'(x) = 2x cos x²

c. f(x) = sin 3x²
Misalkan:
u = 3x² ⇒ u' = 6x
f(x) = sin 3x²
f'(x) = cos u . u'
f'(x) = cos 3x² . 6x
f'(x) = 6x cos 3x²

d. f(x) = sin (2x + 1)
Misalkan:
u = 2x + 1 ⇒ u' = 2
f(x) = sin (2x + 1)
f'(x) = cos u . u'
f'(x) = cos (2x + 1) . 2
f'(x) = 2 cos (2x + 1)

Soal No.4

Carilah turunan f'(x) dari fungsi-fungsi trigonometri dibawah ini :
a. f(x) = cos 3x
b. f(x) = cos x²
c. f(x) = cos 3x²
d. f(x) = cos (2x + 1)

Pembahasan

a. f(x) = cos 3x
Misalkan:
u = 3x ⇒ u' = 3
f(x) = cos 3x
f'(x) = -sin u . u'
f'(x) = -sin 3x . 3
f'(x) = -3 sinx 3x

b. f(x) = cos x²
Misalkan:
u = x² ⇒ u' = 2x
f(x) = cos x²
f'(x) = -sin u . u'
f'(x) = -sin x² . 2x
f'(x) = -2x sin x²

c. f(x) = cos 3x²
Misalkan:
u = 3x² ⇒ u' = 6x
f(x) = cos 3x²
f'(x) = -sin u . u'
f'(x) = -sin 3x² . 6x
f'(x) = -6x sin 3x²

d. f(x) = cos (2x + 1)
Misalkan:
u = 2x + 1 ⇒ u' = 2
f(x) = cos (2x + 1)
f'(x) = -sin u . u'
f'(x) = -sin (2x + 1) . 2
f'(x) = -2 sin (2x + 1)

Soal No.5

Carilah turunan f'(x) dari fungsi-fungsi trigonometri dibawah ini :
a. f(x) = sin (x² + 3x + 1)
b. f(x) = cot (x³ + 3x² + 1)

Pembahasan

a. f(x) = sin (x² + 3x + 1)
Misalkan: u = x² + 3x + 1 ⇒ u' = 2x + 3
f(x) = sin (x² + 3x + 1)
f'(x) = cos u . u'
f'(x) = cos (x² + 3x + 1) . (2x + 3)
f'(x) = (2x + 3) cos (x² + 3x + 1)

b. f(x) = cot (x³ + 3x² + 1)
Misalkan : u = x³ + 3x² + 1 ⇒ u' = 3x² + 6x
f(x) = cot (x³ + 3x² + 1)
f'(x) = -csc² u . u'
f'(x) = -csc² (x³ + 3x² + 1) . (3x² + 6x)
f'(x) = -(3x² + 6x) . csc² (x³ + 3x² + 1)

Soal no.6

Carilah turunan f'(x) dari fungsi-fungsi trigonometri dibawah ini :
a. f(x) = sin x cos 3x
b. f(x) = tan x cos 4x

Pembahasan

a. f(x) = sin x cos 3x
Misal :
u = sin x ⇒ u' = cos x
v = cos 3x ⇒ v' = -3 sin 3x

Turunan dari bentuk fungsi tersebut adalah :
f'(x) = u' . v + u . v'
f'(x) = cos x . cos 3x + sin x . -3 sin 3x
f'(x) = cos x . cos 3x − 3 sin x. sin 3x

b. f(x) = tan x cos 4x
Misal :
u = tan x ⇒ u' = sec²x
v = cos 4x ⇒ v' = -4 sin 4x
Turunan dari bentuk fungsi tersebut adalah :
f'(x) = u' . v + u . v'
f'(x) = sec²x . cos 4x + tan x . -4 sin 4x
f'(x) = sec²x . cos 4x - 4 tan x . sin 4x

Soal No.7

Tentukan turunan pertama dari fungsi berikut :
y =

1 + cos xsin x

Pembahasan

Misal :
u = 1 + cos x ⇒ u' = -sin x
v = sin x ⇒ v' = cos x

Maka :
y' =

u' . v + u . v'v²

y' =

-sin x (sin x) − (1 + cos x) (cos x)sin² x

y' =

-sin² x − cos² x − cos xsin² x

y' =

-(sin² x + cos² x) − cos xsin² x

y' =

-(1) - cos x1 - cos² x

y' =

-(1 + cos x)(1 − cos x).(1 + cos x)

y' =

-11 − cos x

y' =

1cos x - 1

Soal No.8

Tentukan turunan pertama dari fungsi berikut :
y = sin² (2x + 3)

Pembahasan

Misalkan :
g(x) = 2x + 3 ⇒ g'(x) = 2

Rumus turunan untuk fungsi trigonometri berpangkat :
y = c sinⁿ g(x)
y' = c. n sin^n-1 g(x) . cos g(x) . g'(x)

Sehingga : y = sin² (2x + 3)
y = {sin(2x + 3)}²
y' = c. n sin^n-1 g(x) . cos g(x) . g'(x)
y' = 2 sin^2-1 (2x + 3) . cos (2x + 3).(2)
y' = 4 sin (2x + 3) cos (2x + 3)

Soal No.9

Tentukan turunan pertama dari fungsi berikut :
y = cos² (2x² + 3)

Pembahasan

Misalkan :
g(x) = (2x²) + 3 ⇒ g'(x) = 4x

Rumus turunan untuk fungsi trigonometri berpangkat :
y = c cosⁿ g(x)
y' = -c. n cos^n-1 g(x) . sin g(x) . g'(x)

Sehingga :
y = cos² (2x² + 3)
y = {cos(2x² + 3)}²
y' = -c. n cos^n-1 g(x) . sin g(x) . g'(x)
y' = -2 cos^2-1 (2x² + 3) . sin (2x² + 3) . 4x
y' = -8x cos (2x² + 3) . sin (2x² + 3)

Soal No.10

Tentukan turunan pertama dari fungsi berikut :
y = (sin x + cos x)^s

Pembahasan :

Misalkan :
g(x) = sin x + cos x ⇒ g'(x) = cos x - sin x

y = (sin x + cos x)²
y' = n [g(x)]^n-1. g '(x)
y' = 2 (sin x + cos x)^2-1.(cos x − sin x)
y' = 2 (sin x + cos x).(cos x − sin x)
y' = 2 (cos x + sin x).(cos x − sin x)
y' = 2 (cos² x − sin² x)
y' = 2 (cos² x − (1 − cos² x))
y' = 2 (2cos² x − 1)
y' = 4cos² x − 2.